Linear combinations of vectors
We’ll consider a vector an array of numbers:
\[ \begin{pmatrix}1\\5\end{pmatrix}, \begin{pmatrix}1\\-5\\0.1\end{pmatrix},\begin{pmatrix}x\\y\\z\end{pmatrix} \]
What can you do with vectors?
Answer: linear combinations! Which can be viewed analytically or geometrically.
Analytical l.c. : A linear combination is a computation that looks like this:
\[ 2 \mathbf{u}+4\mathbf{v} = 2\begin{pmatrix} 1\\3\end{pmatrix}+4\begin{pmatrix} 1\\-1\end{pmatrix} \]
First multiply the vectors by the scalars, then add the vectors by adding the entries, the result is:
\[ \begin{pmatrix} 2\\6\end{pmatrix}+\begin{pmatrix} 4\\-4\end{pmatrix} = \begin{pmatrix} 6\\2 \end{pmatrix} \]
A generic linear combination looks like this:
\[ a \mathbf{u}+b\mathbf{v} = a\begin{pmatrix} 1\\5\end{pmatrix}+b\begin{pmatrix} 2\\10\end{pmatrix} = \begin{pmatrix}a +2b\\5a +10b \end{pmatrix} \]
where \(a\) and \(b\) are scalars.
If you know how to combine two vectors, you know how to combine three and so on.
Definition 1 The list of vectors \(\mathbf{u}_1,\dots,\mathbf{u}_k\) from \(\mathbb{R}^n\) (i.e. \(\mathbf{u}_i=(u_{i1},\dots,u_{ik})\)), can be linearly combined with numbers \(c_1,\dots,c_k\) as:
\[ c_1\mathbf{u}_1+\dots +c_k\mathbf{u}_k =: \sum_{j=1}^kc_j\mathbf{u}_j=:\mathbf{v} \]
This l.c. is a new vector of \(\mathbb{R}^n\), call it \(\mathbf{v}\).
Let \(\mathbf{a}=\begin{pmatrix} 3\\1\end{pmatrix}\), \(\mathbf{b}=\begin{pmatrix} 1\\2\end{pmatrix}\), \(\mathbf{c}=\begin{pmatrix} -3\\2\end{pmatrix}\). Compute the vector \(\mathbf{v}\) for each case below:
\(\mathbf{v}=-\begin{pmatrix} 3\\4\end{pmatrix}+2\begin{pmatrix} 1\\1\end{pmatrix}\)
\(\mathbf{v}=\mathbf{a}-2\mathbf{b}+\mathbf{c}\).
\(-\mathbf{a}+3\mathbf{b}+\mathbf{v}=\mathbf{c}+\mathbf{a}\)
Geometrical l.c. : A l.c. is performed geometrically using the parallelogram rule:
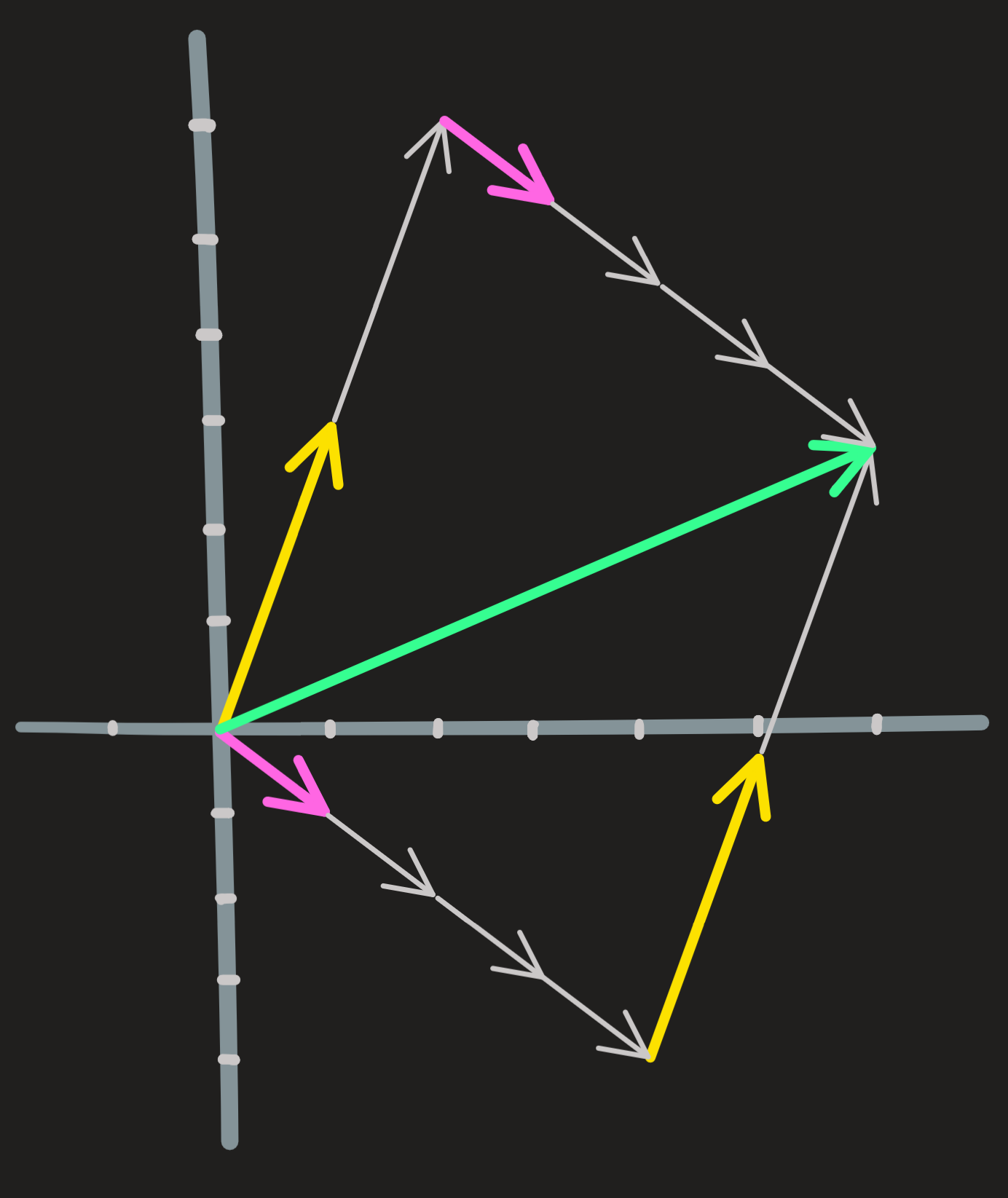
Draw the vectors \(\begin{pmatrix} 3\\4\end{pmatrix}\) and \(\begin{pmatrix} 1\\1\end{pmatrix}\). Then compute the vector \(-\begin{pmatrix} 3\\4\end{pmatrix}+2\begin{pmatrix} 1\\1\end{pmatrix}\) using the parallelogram rule.